モデルの評価
前回はモデルのチューニングまでを済ませたので、続いてモデルの評価に進む。
PyCaretはモデルの評価もあっさり表示してくれる。
# 作成したモデルの評価を行う
evaluate_model(tuned_rf)
-------
Parameters
bootstrap False
ccp_alpha 0.0
criterion mse
max_depth 7
max_features sqrt
max_leaf_nodes None
max_samples None
min_impurity_decrease 0
min_impurity_split None
min_samples_leaf 2
min_samples_split 5
min_weight_fraction_leaf 0.0
n_estimators 290
n_jobs -1
oob_score False
random_state 0
verbose 0
warm_start Falseそのまま出力すると、パラメータに関する情報が出力される。
もしくは選択肢をクリックすることで、コードを書かなくても評価指標を出力してくれる。
今回はコードで出力させる。
# 評価指標を指定して出力する(Feature Importance)
# 説明変数の重要度をグラフ化
plot_model(tuned_rf, 'feature') 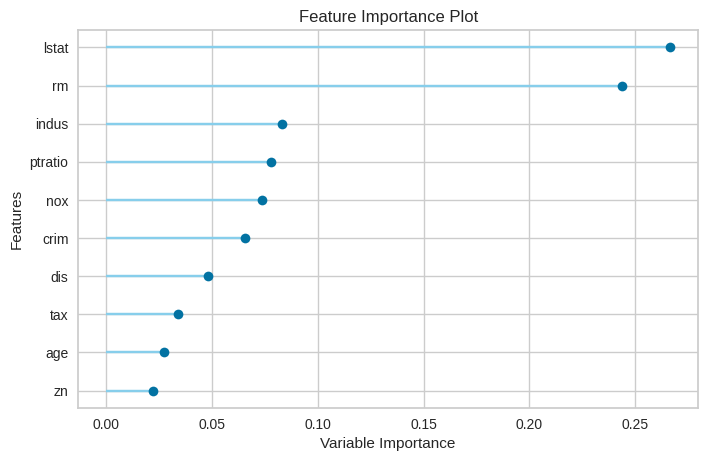
各説明変数の寄与度をグラフ化。どの変数がどの程度予測に影響を及ぼしているかを判断することができる。
# 評価指標を指定して出力する(残差プロット ヒストグラム付き)
plot_model(tuned_rf, "residuals")
残差プロットを出力。ヒストグラム付きで見やすい。予測値と結果の差を把握することができる。
おおむね0付近にプロットされているが、時々飛び抜けて外れたデータが存在しているのが分かる。
# 評価指標を指定して出力する(予測エラープロット)
plot_model(tuned_rf, "error")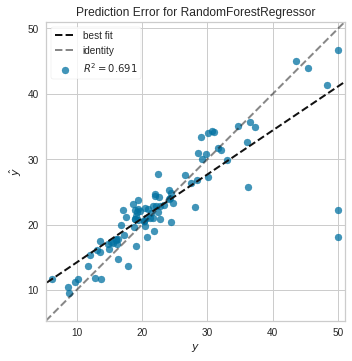
予測エラープロットは、identityに対するズレをR2で表現する。精度が上がってくると、y = xの直線にどんどん近づいていく。
このグラフから、値が大きくなるにつれて精度が悪くなっていくことが分かる。
# 評価指標を指定して出力する(学習曲線)
plot_model(tuned_rf, "learning")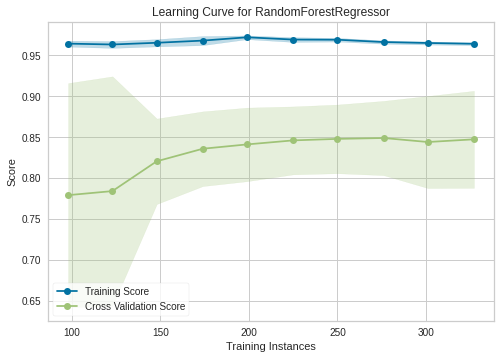
train-trainとtrain-testの予測精度がデータ数に対してどう動くかを視覚化。横軸がデータ数、縦軸は性能を示す。
データ数が増えるほど精度は上がっていくが、一定のところまで来ると精度の上昇が鈍くなっていくことが分かる。
2つのグラフがもし収束すると、性能アップは見込めなくなる。
モデルの確定
final_rf = finalize_model(tuned_rf)
final_rfなんとなく良さそうなので、モデルを確定させる。
確定させたモデルは、呼び出して予測させることができるようになる。
predict_model(final_rf)
-----
Model MAE MSE RMSE R2 RMSLE MAPE
0 Random Forest Regressor 1.4521 3.8375 1.9589 0.9561 0.0882 0.0719
crim zn indus chas nox rm age dis tax ptratio ... rad_2 rad_24 rad_3 rad_4 rad_5 rad_6 rad_7 rad_8 medv Label
0 0.117470 12.5 7.87 0.0 0.524 6.009 82.900002 6.2267 311.0 15.200000 ... 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 18.900000 20.420621
1 0.072440 60.0 1.69 0.0 0.411 5.884 18.500000 10.7103 411.0 18.299999 ... 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 18.600000 21.353809
2 0.614700 0.0 6.20 0.0 0.507 6.618 80.800003 3.2721 307.0 17.400000 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 30.100000 27.714919
3 0.071650 0.0 25.65 0.0 0.581 6.004 84.099998 2.1974 188.0 19.100000 ... 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 20.299999 20.365038
4 0.130580 0.0 10.01 0.0 0.547 5.872 73.099998 2.4775 432.0 17.799999 ... 0.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 20.400000 20.060681
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
86 4.812130 0.0 18.10 0.0 0.713 6.701 90.000000 2.5975 666.0 20.200001 ... 0.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 16.400000 16.409644
87 0.013600 75.0 4.00 0.0 0.410 5.888 47.599998 7.3197 469.0 21.100000 ... 0.0 0.0 1.0 0.0 0.0 0.0 0.0 0.0 18.900000 19.679399
88 18.811001 0.0 18.10 0.0 0.597 4.628 100.000000 1.5539 666.0 20.200001 ... 0.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 17.900000 15.351710
89 1.232470 0.0 8.14 0.0 0.538 6.142 91.699997 3.9769 307.0 21.000000 ... 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 15.200000 16.423641
90 0.028990 40.0 1.25 0.0 0.429 6.939 34.500000 8.7921 335.0 19.700001 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 26.600000 25.419922新たにlabel列が作られ、予測が行われる。
予測
未見データに対して予測を実行してみる
predictions = predict_model(final_rf, data = boston_data_unseen)
print(predictions)
-----
Model MAE MSE RMSE R2 RMSLE MAPE
0 Random Forest Regressor 1.6933 6.3746 2.5248 0.6631 0.1712 0.1229
crim zn indus chas nox rm age dis rad tax ptratio \
0 4.75237 0.0 18.10 0 0.713 6.525 86.5 2.4358 24 666 20.2
1 4.66883 0.0 18.10 0 0.713 5.976 87.9 2.5806 24 666 20.2
2 8.20058 0.0 18.10 0 0.713 5.936 80.3 2.7792 24 666 20.2
3 7.75223 0.0 18.10 0 0.713 6.301 83.7 2.7831 24 666 20.2
4 6.80117 0.0 18.10 0 0.713 6.081 84.4 2.7175 24 666 20.2
5 4.81213 0.0 18.10 0 0.713 6.701 90.0 2.5975 24 666 20.2
6 3.69311 0.0 18.10 0 0.713 6.376 88.4 2.5671 24 666 20.2
7 6.65492 0.0 18.10 0 0.713 6.317 83.0 2.7344 24 666 20.2
8 5.82115 0.0 18.10 0 0.713 6.513 89.9 2.8016 24 666 20.2
9 7.83932 0.0 18.10 0 0.655 6.209 65.4 2.9634 24 666 20.2
10 3.16360 0.0 18.10 0 0.655 5.759 48.2 3.0665 24 666 20.2
11 3.77498 0.0 18.10 0 0.655 5.952 84.7 2.8715 24 666 20.2
12 4.42228 0.0 18.10 0 0.584 6.003 94.5 2.5403 24 666 20.2
13 15.57570 0.0 18.10 0 0.580 5.926 71.0 2.9084 24 666 20.2
14 13.07510 0.0 18.10 0 0.580 5.713 56.7 2.8237 24 666 20.2
15 4.34879 0.0 18.10 0 0.580 6.167 84.0 3.0334 24 666 20.2
16 4.03841 0.0 18.10 0 0.532 6.229 90.7 3.0993 24 666 20.2
17 3.56868 0.0 18.10 0 0.580 6.437 75.0 2.8965 24 666 20.2
18 4.64689 0.0 18.10 0 0.614 6.980 67.6 2.5329 24 666 20.2
19 8.05579 0.0 18.10 0 0.584 5.427 95.4 2.4298 24 666 20.2
20 6.39312 0.0 18.10 0 0.584 6.162 97.4 2.2060 24 666 20.2
21 4.87141 0.0 18.10 0 0.614 6.484 93.6 2.3053 24 666 20.2
22 15.02340 0.0 18.10 0 0.614 5.304 97.3 2.1007 24 666 20.2
23 10.23300 0.0 18.10 0 0.614 6.185 96.7 2.1705 24 666 20.2
24 14.33370 0.0 18.10 0 0.614 6.229 88.0 1.9512 24 666 20.2
25 5.82401 0.0 18.10 0 0.532 6.242 64.7 3.4242 24 666 20.2
26 5.70818 0.0 18.10 0 0.532 6.750 74.9 3.3317 24 666 20.2
27 5.73116 0.0 18.10 0 0.532 7.061 77.0 3.4106 24 666 20.2
28 2.81838 0.0 18.10 0 0.532 5.762 40.3 4.0983 24 666 20.2
29 2.37857 0.0 18.10 0 0.583 5.871 41.9 3.7240 24 666 20.2
30 3.67367 0.0 18.10 0 0.583 6.312 51.9 3.9917 24 666 20.2
31 5.69175 0.0 18.10 0 0.583 6.114 79.8 3.5459 24 666 20.2
32 4.83567 0.0 18.10 0 0.583 5.905 53.2 3.1523 24 666 20.2
33 0.15086 0.0 27.74 0 0.609 5.454 92.7 1.8209 4 711 20.1
34 0.18337 0.0 27.74 0 0.609 5.414 98.3 1.7554 4 711 20.1
35 0.20746 0.0 27.74 0 0.609 5.093 98.0 1.8226 4 711 20.1
36 0.10574 0.0 27.74 0 0.609 5.983 98.8 1.8681 4 711 20.1
37 0.11132 0.0 27.74 0 0.609 5.983 83.5 2.1099 4 711 20.1
38 0.17331 0.0 9.69 0 0.585 5.707 54.0 2.3817 6 391 19.2
39 0.27957 0.0 9.69 0 0.585 5.926 42.6 2.3817 6 391 19.2
40 0.17899 0.0 9.69 0 0.585 5.670 28.8 2.7986 6 391 19.2
41 0.28960 0.0 9.69 0 0.585 5.390 72.9 2.7986 6 391 19.2
42 0.26838 0.0 9.69 0 0.585 5.794 70.6 2.8927 6 391 19.2
43 0.23912 0.0 9.69 0 0.585 6.019 65.3 2.4091 6 391 19.2
44 0.17783 0.0 9.69 0 0.585 5.569 73.5 2.3999 6 391 19.2
45 0.22438 0.0 9.69 0 0.585 6.027 79.7 2.4982 6 391 19.2
46 0.06263 0.0 11.93 0 0.573 6.593 69.1 2.4786 1 273 21.0
47 0.04527 0.0 11.93 0 0.573 6.120 76.7 2.2875 1 273 21.0
48 0.06076 0.0 11.93 0 0.573 6.976 91.0 2.1675 1 273 21.0
49 0.10959 0.0 11.93 0 0.573 6.794 89.3 2.3889 1 273 21.0
50 0.04741 0.0 11.93 0 0.573 6.030 80.8 2.5050 1 273 21.0
black lstat medv Label
0 50.92 18.13 14.1 15.209421
1 10.48 19.01 12.7 14.967431
2 3.50 16.94 13.5 14.108571
3 272.21 16.23 14.9 15.317036
4 396.90 14.70 20.0 18.092477
5 255.23 16.42 16.4 16.409644
6 391.43 14.65 17.7 18.412431
7 396.90 13.99 19.5 18.845325
8 393.82 10.29 20.2 20.064201
9 396.90 13.22 21.4 20.300518
10 334.40 14.13 19.9 20.175202
11 22.01 17.15 19.0 17.727792
12 331.29 21.32 19.1 17.414715
13 368.74 18.13 19.1 17.879081
14 396.90 14.76 20.1 18.891600
15 396.90 16.29 19.9 18.839092
16 395.33 12.87 19.6 20.089245
17 393.37 14.36 23.2 19.800097
18 374.68 11.66 29.8 26.072939
19 352.58 18.14 13.8 15.726636
20 302.76 24.10 13.3 15.672915
21 396.21 18.68 16.7 17.659343
22 349.48 24.91 12.0 14.355467
23 379.70 18.03 14.6 16.021638
24 383.32 13.11 21.4 19.599364
25 396.90 10.74 23.0 21.016906
26 393.07 7.74 23.7 24.304404
27 395.28 7.01 25.0 25.636513
28 392.92 10.42 21.8 20.748658
29 370.73 13.34 20.6 20.338750
30 388.62 10.58 21.2 20.788358
31 392.68 14.98 19.1 19.187453
32 388.22 11.45 20.6 20.650867
33 395.09 18.06 15.2 16.330112
34 344.05 23.97 7.0 15.928464
35 318.43 29.68 8.1 16.034774
36 390.11 18.07 13.6 16.282222
37 396.90 13.35 20.1 19.144682
38 396.90 12.01 21.8 20.610437
39 396.90 13.59 24.5 20.730792
40 393.29 17.60 23.1 20.571572
41 396.90 21.14 19.7 19.562634
42 396.90 14.10 18.3 20.276365
43 396.90 12.92 21.2 20.597973
44 395.77 15.10 17.5 19.720113
45 396.90 14.33 16.8 19.943801
46 391.99 9.67 22.4 21.781099
47 396.90 9.08 20.6 20.061667
48 396.90 5.64 23.9 24.676981
49 393.45 6.48 22.0 22.546324
50 396.90 7.88 11.9 19.396725 ふんわりいい感じに予測できているように見える。ひとまずこれでモデルの作成とテストは完成。
続いて、毎回モデル作成を行うと重たくてしょうがないのでモデルを保存する。
# modelの保存
save_model(final_rf, model_name = 'final_rf_model')
%ls # リスト表示のマジックコマンド指定したファイル名でモデルが保存される。呼び出したい時は
# モデルの召喚
load_tuned_rf_model = load_model(model_name = "final_rf_model")
load_tuned_rf_modelこのようにする。
続きは次回。